此教程通过简单且易于理解的实例介绍了Q-learning的概念知识,例子描述了一个智能体通过非监督学习的方法对未知的环境进行学习。
假设我们的楼层内共有5个房间,房间之间通过一道门相连,正如下图所示。我们将房间编号为房间0到房间4,楼层的外部可以被看作是一间大房间,编号为5。注意到房间1和房间4可以直接通到房间5。
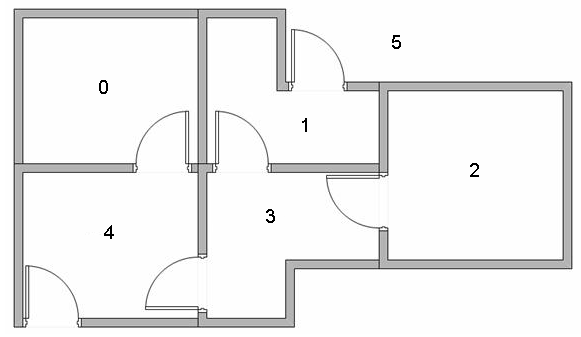
我们可以用图来表示上述的房间,将每一个房间看作是一个节点,每一道门看作是一条边(链路)。
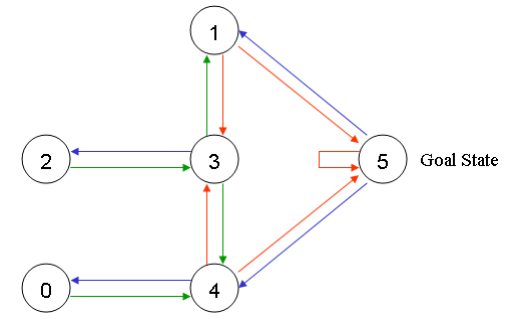
在这个例子中,我们可以在任意一间房间中放置一个智能体(Agent),并期望该智能体能够从该房间开始走出这栋楼。换句话说,智能体的目的地是房间5。为了设置这间房间作为目标,我们为每一道门(节点之间的边)赋予一个奖励值。能够直接通到目标房间的门赋予一及时奖励值100,而其他的未与目标房间直接相连的门赋予奖励值0。因为每一道门都有两个方向,因此,每一道门在图中将描述为两个箭头。如下所示:

当然,其他所有直接通到目标房间5的奖励值是100,从房间5到房间5的奖励值也是100。在Q-Learing中,学习的目标是达到具有最高奖励值的状态,因此,如果智能体到达了目标位置,它将永远的留在那儿。这种类型的目标被称为“吸收目标”,i.e.整个系统的最终收敛目标。
想象我们的智能体是一个不会说话的虚拟机器人,但是它可以从经验中学习。智能体能够从一个房间到达另外一个房间,但是它对周围的环境一无所知,它不知道怎么走能够通到楼层外面(房间5)。
假设我们想对智能体从某一个房间中撤退的过程进行建模,现在,我们假设智能体在房间2内,我们希望智能体通过学习到达房间5。
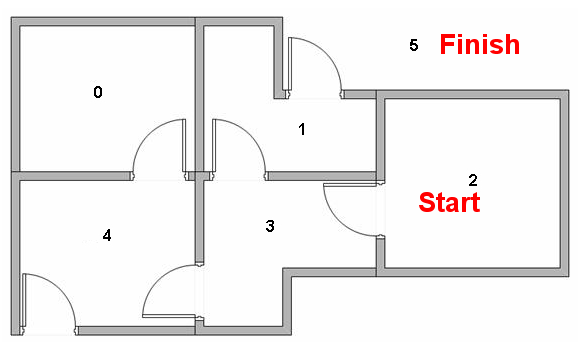
Q-学习中的术语包括状态(state)和动作(action)。
我们将每一个房间称为一个“状态”,智能体从一个房间到另一个房间的移动过程称为“动作”。在我们的示意图中,状态被描述为节点,动作被描述成箭头。

假设智能体处于状态2,那么,它从状态2能够直接到达状态3,因为状态2和状态3相连。然而,智能体从状态2不能直接到达状态1,因为在房间2和房间1之间没有直接相通的门,也即没有箭头存在。从状态3,智能体要么到达状态1,要么到达状态4,抑或着返回到状态2。如果智能体处于状态4,那么它有3种可能的动作,即到达状态0,、5或3。如果智能体在状态1,它能够到达状态5或者状态3。从状态0,它只能到达状态4。
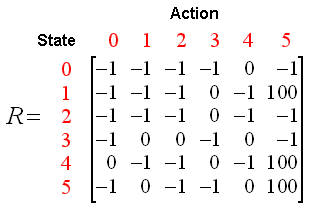
我们可以将状态图和即时奖励值填入到下面的奖励表中,即矩阵R:
(表中的-1代表空值,不允许通过)
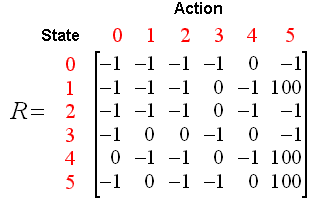
现在,我们再增加一个相似的矩阵Q,代表智能体从经验中所学到的知识。矩阵Q的行代表智能体当前的状态,列代表到达下一个状态的可能的动作。
因为智能体在最初对环境一无所知,因此矩阵Q被初始化为0。在这个例子中,为了阐述方便,我们假设状态的数量是已知的(设为6)。如果我们不知道有多少状态时,矩阵Q在最初被设为只有一个元素。如果新的状态一旦被发现,对矩阵Q增加新的行和新的列非常简单。
Q-学习的转换规则非常简单,为下面的式子:
Q(state, action)=R(state, action) + Gamma * Max(Q[next state, all actions])
***********************************************************
PS:实际上,我在一些教材上,或者别的博客看到的公式大多都是下面这样的:

原文作者的公式只是括号中的一部分,相当于把α取值为0。
***********************************************************
依据这个公式,矩阵Q中的一个元素值就等于“矩阵R中相应元素的值”与“学习变量Gamma”乘以“到达下一个状态的所有可能动作的最大奖励值”的总和。
我们的智能体将从经验中学习,不需要教师指导信号(这被称为非监督学习)。智能体将从一个状态到另一个状态进行探索,直到它到达目标状态时停止。我们将每一次探索作为一次经历,每一次经历包括智能体从初始状态到达目标状态的过程。每次智能体到达了目标状态,程序将会转向下一次探索。
Q-Learning算法的计算过程如下:
1、设置参数Gamma,以及矩阵R中的环境奖励值;
2、初始化Q矩阵为0;
3、对每一次经历:
随机选择一个状态;
Do while 目标状态未到达
对当前状态的所有可能的动作中,选择一个可能的动作;
使用这个可能的动作,到达下一个状态;
对下一个状态,基于其所有可能的动作,获得最大的Q值;
计算:Q(state, action)=R(state, action) + Gamma * Max(Q[next state, all actions])
设置下一个状态作为当前状态;
End For
智能体利用上述的算法从经验中学习,每一次经历等价于一次训练。在每一次训练中,智能体对环境进行探索(用矩阵R表示),并且其一旦到达目标状态,就得到奖励值。训练的目的是增强智能体的大脑,用矩阵Q表示。越多的训练结果将导致更优的矩阵Q。在这种情况下,如果矩阵Q已经被增强,那么智能体就不会四处盲目的探索,而是会找到最快的路线到达目标状态。
参数Gamma的取值在0到1之间(0<=Gamma<=1),如果Gamma越接近于0,智能体更趋向于仅仅考虑即时奖励;如果Gamma更接近于1,智能体将以更大的权重考虑未来的奖励。
************************************************************
PS:除此之外,在上一个补充说明部分的公式中,参数α也有类似的意义,不过α是对历史奖励的权衡,γ是对未来奖励的权衡。
************************************************************
为了使用矩阵Q,智能体仅仅简单地跟踪从起始状态到目标状态的状态序列。这个算法会为当前状态寻找在矩阵Q中具有最高奖励值的动作。
利用矩阵Q的算法如下:
1、设置当前状态=初始状态;
2、从当前状态开始,寻找具有最高Q值的动作;
3、设置当前状态=下一个状态;
4、重复步骤2和3,直到当前状态=目标状态。
上述的算法将返回从初始状态到目标状态的状态序列。
为了理解Q-学习算法是怎样工作的,我们通过分析少量的例子进行分析。
我们设置学习率Gamma等于0.8,初始的状态是房间1。
初始的矩阵Q作为一个零矩阵,如下:

观察R矩阵的第二行(状态1),对状态1来说,存在两个可能的动作:到达状态3,或者到达状态5。通过随机选择,我们选择到达状态5。
现在,让我们想象如果我们的智能体到达了状态5,将会发生什么?观察R矩阵的第六行,有3个可能的动作,到达状态1,4或者5。
根据Q(state, action) = R(state, action) + Gamma * Max[Q(next state, all actions)],我们计算如下:
Q(1, 5) = R(1, 5) + 0.8 * Max[Q(5, 1), Q(5, 4), Q(5, 5)] = 100 + 0.8 * 0 = 100
由于矩阵Q此时依然被初始化为0,Q(5, 1), Q(5, 4), Q(5, 5)全部是0,因此,Q(1, 5)的结果是100。
因为状态5是目标状态,因此我们算是已经完成了一次尝试。我们的智能体的大脑中现在包含了一个更新后的Q矩阵。

PS:原作者的这个图有点错误,100应该是在Q(1, 5)的位置,而不是Q(2, 5)。
对于下一次训练,我们随机选择一个初始状态,这一次,我们选择状态3作为我们的初始状态。
观察R矩阵的第4行,有3个可能的动作,到达状态1,2和4。我们随机选择到达状态1作为当前状态的动作。
现在,我们想象我们在状态1,观察矩阵R的第2行,具有2个可能的动作:到达状态3或者状态5。现在我们计算Q值:
Q(3, 1) = R(3, 1) + 0.8 * Max[Q(1, 2), Q(1, 5)] = 0 + 0.8 * Max(0, 100) = 80
我们使用上一次尝试中更新的矩阵Q得到:Q(1, 3) = 0 以及 Q(1, 5) = 100。因此,计算的结果是Q(3,1)=80。现在,矩阵Q变为:

下一个状态1变成了当前状态。由于状态1不是目标状态,我们重复Q学习算法中的循环过程。
因此,我们从当前状态1开始选择,此时有2个可能的动作:到达状态3或者状态5。我们幸运地选择到达了状态5。

现在,想象我们处于状态5,有3个可能的动作:到达状态1,4或5。我们计算Q值如下:
Q(1, 5) = R(1, 5) + 0.8 * Max[Q(5, 1), Q(5, 4), Q(5, 5)] = 100 + 0.8 * 0 = 100
更新后的矩阵Q中,Q(5, 1), Q(5, 4), Q(5, 5)依然是0,故Q(1, 5)的值是100,这并没有改变矩阵Q。
因为状态5是目标状态,我们完成了这次尝试。我们的智能体大脑中包含的矩阵Q更新为如下所示:

按照这样的规律,如果我们的智能体通过多次的经历学到了更多的知识,Q矩阵中的值会达到一收敛状态,如下:

通过对Q中所有的非零值缩小一定的百分比,可以对其进行标准化,结果如下:

一旦矩阵Q接近于收敛状态,我们就认为智能体已经学习到了到达目标状态的最佳路径。
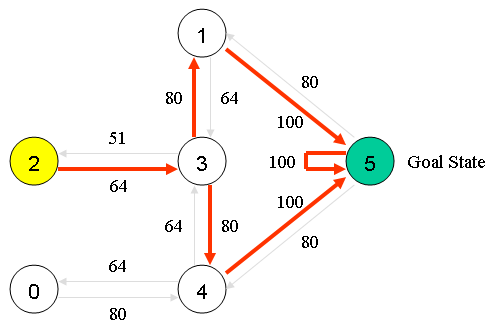
例如,从初始状态2,智能体在矩阵Q的指导下进行移动:
在状态2时,由矩阵Q中最大的值可知下一个动作应该是到达状态3;
在状态3时,矩阵Q给出的建议是到达状态1或者4,我们任意选择,假设选择了到达状态1;
在状态1时,矩阵Q建议到达状态5;
因此,智能体的移动序列是2-3-1-5。
其实,Q矩阵包含的内容就是我们在当前状态下,采取每一个动作对应的收益期望,智能体在决策时自然会选择能够获得更高收益的动作。
import numpy as np
# Q 矩阵初始化为0
q = np.matrix(np.zeros([6, 6]))
# Reward 矩阵为提前定义好的。 类似与HMM的生成矩阵。-1表示无相连接的边
r = np.matrix([[-1, -1, -1, -1, 0, -1],
[-1, -1, -1, 0, -1, 100],
[-1, -1, -1, 0, -1, -1],
[-1, 0, 0, -1, 0, -1],
[ 0, -1, -1, 0, -1, 100],
[-1, 0, -1, -1, 0, 100]])
# hyperparameter
#折扣因子
gamma = 0.8
#是否选择最后策略的概率
epsilon = 0.4
# the main training loop
for episode in range(25):
print('first episode',episode)
# random initial state
state = np.random.randint(0, 6)
print('state',state)
# 如果不是最终转态
while (state != 5):
# 选择可能的动作
# Even in random case, we cannot choose actions whose r[state, action] = -1.
possible_actions = []
possible_q = []
for action in range(6):
if r[state, action] >= 0:
possible_actions.append(action)
possible_q.append(q[state, action])
# Step next state, here we use epsilon-greedy algorithm.
action = -1
if np.random.random() < epsilon:
# choose random action
action = possible_actions[np.random.randint(0, len(possible_actions))]
print('actionif',action)
else:
# greedy
action = possible_actions[np.argmax(possible_q)]
print('actionelse',action)
# Update Q value
q[state, action] = r[state, action] + gamma * q[action].max()
# Go to the next state
state = action
print("Training episode: %d" % episode)
print(q)
print("------------------------------------------------")
'''
# Display training progress
if episode % 10 == 0:
print("------------------------------------------------")
print("Training episode: %d" % episode)
print(q)
'''2.此例的简洁代码(功能与结论一样):
import numpy as np
import random
# 初始化矩阵
Q = np.zeros((6, 6))
Q = np.matrix(Q)
# 回报矩阵R
R = np.matrix([[-1,-1,-1,-1,0,-1],[-1,-1,-1,0,-1,100],[-1,-1,-1,0,-1,-1],[-1,0,0,-1,0,-1],[0,-1,-1,0,-1,100],[-1,0,-1,-1,0,100]])
# 设立学习参数
γ = 0.8
# 训练
for i in range(2000):
# 对每一个训练,随机选择一种状态
state = random.randint(0, 5)
while True:
# 选择当前状态下的所有可能动作
r_pos_action = []
for action in range(6):
if R[state, action] >= 0:
r_pos_action.append(action)
next_state = r_pos_action[random.randint(0, len(r_pos_action) - 1)]
Q[state, next_state] = R[state, next_state] + γ *(Q[next_state]).max() #更新
state = next_state
# 状态4位最优库存状态
if state==5:
break
print(Q/5)
3.golang版:
package main
import ("fmt"
"time"
"math/rand")
func argMaxValue(arr [] float64) float64{
maxVal:=arr[0]
for i:=1;i < len(arr);i++{
if maxVal < arr[i]{
maxVal=arr[i]
}//if maxVal
}//for
return maxVal
}//argMaxValue
func Duplicate(s []int) (ret []int) {
//fmt.Printf("s :%+v\n", s)
tmpM := make(map[int]int)
for _, v := range s {
tmpM[v] = 1
}
s = []int{}
for i, _ := range tmpM {
s = append(s, i)
}
return s
}
func main(){
var gamma float64=0.8
Q:=[][]float64{
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
{0,0,0,0,0,0},
}
R:=[][]float64{
{-1,-1,-1,-1,0,-1},
{-1,-1,-1,0,-1,100},
{-1,-1,-1,0,-1,-1},
{-1,0,0,-1,0,-1},
{0,-1,-1,0,-1,100},
{-1,0,-1,-1,0,100},
}
i:=0
state:=0
next_state:=0
for i=0;i < 2000;i++{
rand.Seed(time.Now().UnixNano())
state=rand.Intn(6)
for{
var r_pos_action [] int
action:=0
for action=0;action<6;action++{
if R[state][action] >=0{r_pos_action=append(r_pos_action,action)}
}//for action
r_pos_action=Duplicate(r_pos_action)
tempIndex:=len(r_pos_action)-1
next_state=r_pos_action[tempIndex]
Q[state][next_state]=R[state][next_state]+gamma*argMaxValue(Q[next_state])
state=next_state
if state==5{break}
}//for
}//for i=0;
fmt.Println("Q",Q)
}//main